The Paradox of the Black Feminist Panda: Applying Godel's Incompleteness Theorem to Intersectionality
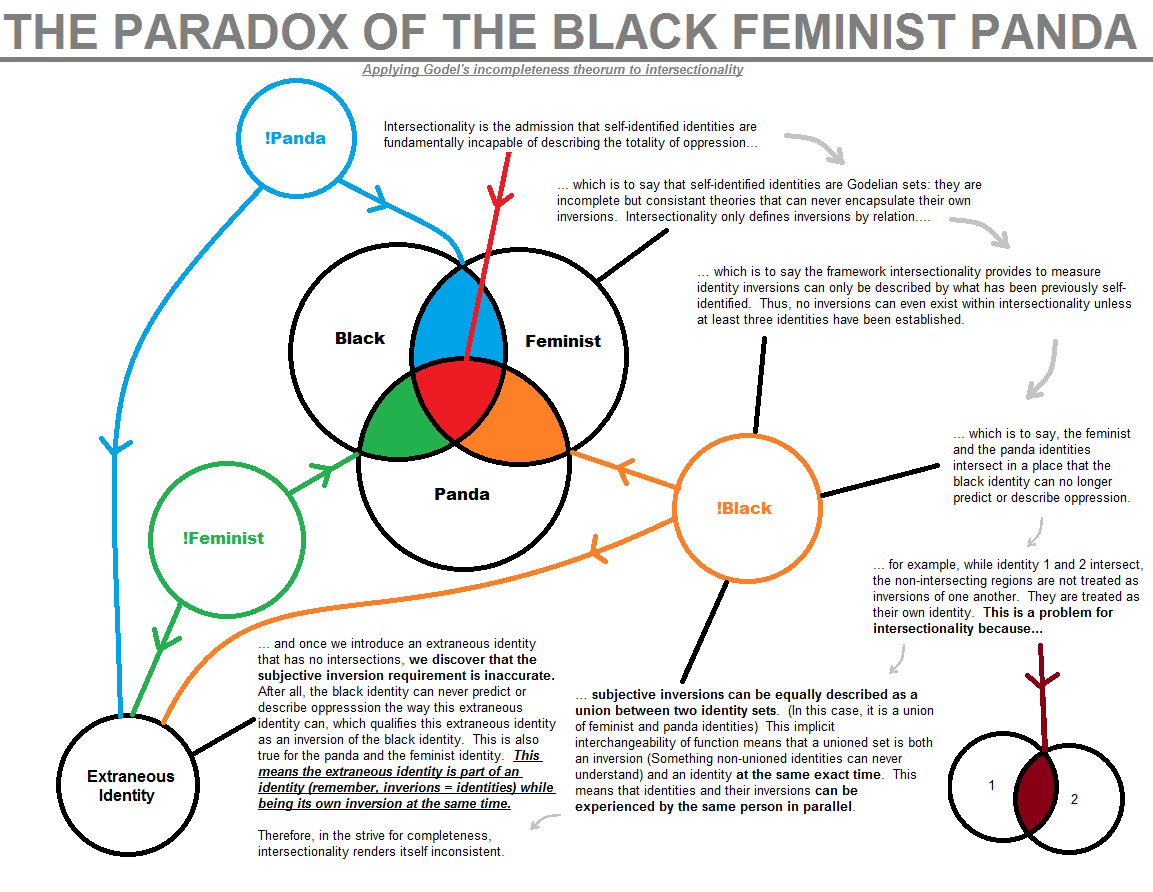
Intersectionality is the admission that self-identified identities are fundamentally incapable of describing the totality of oppression. This means that self-identified identities are Godelian sets: they are incomplete but consistent theories that can never encapsulate their own inversions.
lntersectionality only defines inversions by relation, which is to say the framework intersectionality provides to measure identity inversions can only be described by what has been previously self-identified. Thus, no inversions can even exist within intersectionality unless at least three identities have been established.
For example, the feminist and the panda identities intersect in a place that the black identity can no longer predict or describe oppression. (Additionally, if identity 1 and 2 intersect, the non-intersecting regions are not treated as inversions of one another. They are treated as their own identity.) This is a problem for intersectionality because subjective inversions can be equally described as a union between two identity sets. (In this case, it is a union of feminist and panda identities) This implicit interchangeability of function means that a unioned set is both an inversion (Something non-unioned identities can never understand) and an identity at the same exact time. This means that identities and their inversions can be experienced by the same person in parallel.
Once we introduce an extraneous identity that has no intersections, we discover that the subjective inversion requirement is inaccurate. Alter all, the black identity can never predict or describe oppression the way this extraneous identity can, which qualifies this extraneous identity as an inversion of the black identity. This is also true for the panda and the feminist identity. This means the extraneous identity is part of an identity (remember, inversions = identities) while being its own inversion at the same time.
Therefore, in the strive for completeness, intersectionality renders itself inconsistent.
Proof:
Let theories be a set of theorems.
Let a theorem be a set of proofs that predict and detect oppression.
Let intersectionality imply inversions (!) to be:
- The intersections (∩) of the complement (c) of a theory with its overlapping theories and non-overlapping theories.
- The absolute complement of a theory and all non-overlapping theories.
Let intersectionality deny complements of a theory as a complete theory.
Let intersectionality treat all intersecting theories as new theories.
Let A, C, D be overlapping theories, thus:
Let D = B ∩ C
Let E = C ∩ A
Let F = A ∩ B
Thus, inversions can be defined as:
!A = (A ∩ B)c ∩ C
!B = (B ∩ C)c ∩ A
!C = (C ∩ A)c ∩ B
Thus:
!A = D
!B = E
!C = F
But:
(A ∩ B)c ∩ C = B ∩ C
(B ∩ C)c ∩ A = C ∩ A
(C ∩ A)c ∩ B = A ∩ B
This is logically false since B ∩ C contains not just (A ∩ B)c ∩ C, but also A ∩ B ∩ C.
Intersectionality's implications of inversion, then, is false.
To further demonstrate the point, let X be a different theory of oppression that has no intersecting theorems. Thus:
Ø = X ∩ A
Ø = X ∩ B
Ø = X ∩ C
Ø = X ∩ D
Ø = X ∩ E
Ø = X ∩ F
Thus:
X ∉ B ∩ C
X ∉ C ∩ A
X ∉ A ∩ B
However, due to the second rule of inversion, X is part of all inversions. Thus:
!A = D
Ø = X ∩ D
Ø = X ∩ (B ∩ C)
But:
!A = (A ∩ B)c ∩ C
Ø = X ∩ !A
Ø = X ∩ (A ∩ B)c ∩ C
Is a false statement.